


 |
Home / Soft- & Freeware / Stukre / Publication |
This page is only available in german language.
1. Einführung
Aus verfahrenstechnischen und/oder praktischen Gesichtspunkten ergeben sich häufig Vorteile bei einer Anordnung von Stutzen im Krempenbereich gewölbter Böden. Aufgrund der in diesen Bereichen komplexen Verläufen der Beanspruchungen ist eine Bemessung derartiger Stutzenanschlußstellen mittels mathematisch geschlossener Ansätze bestenfalls mit sehr großem Aufwand möglich. Eine Ermittlung der Beanspruchungen am Stutzenanschluß mittels Finiter-Elementberechnungen in jedem Einzelfall stellt im Hinblick auf den Kostenanteil des Konstruktionsteils "Stutzen" einen unvertretbaren Zeit- und Kostenaufwand dar. Zudem sind bei kleinen und mittelständischen Unternehmen in aller Regel die erforderlichen Rechnerkapazitäten, Rechenprogramme und schalentheoretischen Kenntnisse für die Durchführung und Ergebnisbewertung nicht vorhanden.
In zwei Forschungsvorhaben [1, 2] wurden die für die Bemessung maßgebenden Beanspruchungen von Stutzenanschlußstellen im Krempenbereich mit einer elastischen Parameterstudie mit Finiten Elementen ermittelt. Der Parameterbereich dieser Studie umfaßte dabei den baupraktisch bedeutsamen Bereich der Abmessungsverhältnisse. Die Ergebnisse der elastische Parameterstudie wurden mit Versuchen an zwei Klöpperböden bestätigt und erlauben sowohl die statische Bemessung als auch eine Absicherung gegen Ermüdungsbrüche derartiger Stutzenanschlußstellen für die Lastfälle Innendruck, Axiallast, Umfangs- und Radialmoment am Stutzenende. Die große Datenmenge, die bei der Auswertung der Parameterstudie anfiel, führte zu einer Vielzahl von Bemessungsdiagrammen. Zur Vereinfachung der Handhabung dieser Datenmenge wurde ein frei verfügbares Interpolationsprogramm für die Betriebssysteme DOS, Windows3.x, Windows95 und WindowsNT entwickelt, welches die maßgebenden Beanspruchungen für beliebige Abmessungsverhältnisse innerhalb des Parameterbereiches aus den 'exakten' Ergebnissen der einzelnen Berechnungsläufe ermittelt und darstellt.
Die Ergebnissen dieser Forschungsvorhaben ersetzen die individuelle Schalenberechnung durch eine einfache Handrechnung und reduzieren somit die Kosten und den Zeitaufwand für den Festigkeitsnachweis von Stutzen im Krempenbereich von Klöpper- und Korbbogenböden auf ein wirtschaftlich vertretbares Maß;. Das ermöglicht kleinen und mittelständischen Unternehmen gleichberechtigt am Markt teilzunehmen, der sonst Großunternehmen vorbehalten wäre.
2. Parameterstudie
Die Parameter, die im folgenden zur Beschreibung der Geometrie eines Stutzenanschlusses verwendet werden, sind in Bild 1 dargestellt. Der linke Teil der Tab. 1 gibt die berechneten Behälterformen der Klöpperbodenform an. Die unterstrichenen Kombinationen kennzeichnen die Behälterformen, für die zusätzliche Berechnungen an Korbbogenböden durchgeführt wurden. Bei jeder Behälterform wurden alle 24 Wanddickenkombinationen entsprechend den beiden rechten Spalten der Tab. 1 berechnet. Eine Ausnahme bildete der Klöpperboden mit ca/Da=0.485, di/Da=0.05, se/Da=0.013 und ss/se=2.0, der infolge numerischer Schwierigkeiten beim Systemaufbau nicht erzeugt werden konnte.
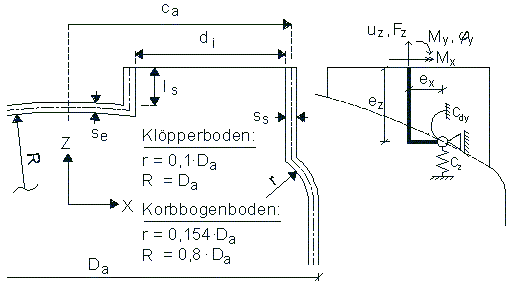
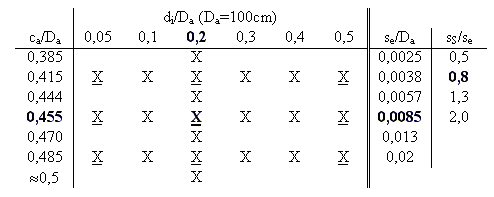
Die Stutzenlage von ca/Da» 0.5 beschreibt die Situation, bei der die Schalenmittelfläche des Stutzens bei y=0 eine Fortsetzung der Schalenmittelfläche des zylindrischen Behälterteils bildet (eigentlich ca=0.5×[Da-se]). Für jede Behältergeometrie wurden die Lastfälle Innendruck (unter Berücksichtigung der Deckelkraft am Stutzenende), Axiallast, Umfangs- und Radialmoment am Stutzenende berechnet. Die in der Tabelle 1 fett dargestellten Geometrieparameter kennzeichnen den Bezugsbehälter, auf den die Ergebnisse der Parameterstudie normiert wurden.
Die Stutzen werden mit der Mindestlänge nach [3] abgebildet. Wegen der großen Membransteifigkeit der an den Stutzen anschließenden Rohrleitungen wird ein ebenes Stutzenende idealisiert. Zur Berücksichtigung der geringen Querschnitts- und Biegesteifigkeit der Schale der angeschlossenen Rohrleitungen werden die Verschiebungen und Verdrehungen der Stutzenendknoten innerhalb dieser Ebene nicht behindert. Der Verschneidungsbereich der Schalen wird wegen der dort auftretenden Maximalwerte der Beanspruchungen aus der Diskontinuität des Stutzenanschlusses mit einem feinen Elementraster abgebildet (vgl. Bild 2). Zur Ermittlung des geeigneten Elementtyps und zur Festlegung einer sinnvollen Elementverfeinerung wurden Vorstudien mit einer Bewertung der Konvergenz durchgeführt. Die Berechnungen der Parameterstudie wurden mit ANSYS, Version 4.3 mit dem Schalenelement Shell63 im feinen und groben Elementraster und mit den Elementen Shell63 und Shell48 im Übergangsbereich durchgeführt. Diese Schalenelemente idealisieren die Schalenmittelfläche und berücksichtigen die Schubnachgiebigkeit rechtwinklig zur Elementebene.
Die Berechnungen wurden zur Reduzierung der Rechenzeit am halben System unter Berücksichtigung der Symmetrie- und Antimetriebedingungen durchgeführt. In den Fällen, in denen die Störspannungen aus dem Stutzenanschluß bis zur Ebene bei x=0 weitestgehend abgeklungen waren, genügte die Idealisierung eines Auschnittes von 90 Grad.

Zur Berücksichtigung der gegenseitigen Stützung der Schalen im Volumen der Verschneidung werden die Beanspruchungen der Schalen an den maßgebenden Schnitten ausgewertet. Diese maßgebenden Schnitte befinden sich im Abstand der halben Wanddicke von der Schnittlinie der Schalenmittelflächen (vgl. Bild 2).
3. Statische Versuche
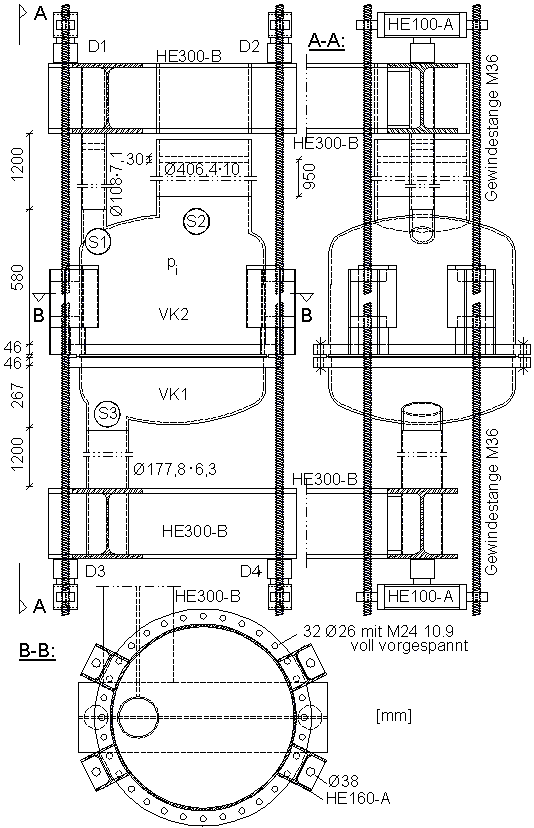
Die statischen Versuche wurden an zwei Klöpperböden mit insgesamt 3 eingeschweißten Stutzen durchgeführt. Dabei wurden die Lastfälle Innendruck, Axiallast, Umfangs- und Radialmoment am Stutzenende jeweils mehrfach aufgebracht. Die beiden Klöpperböden wurden gegeneinander verspannt und abgedichtet. Der Innendruck wurde über eine Wasserfüllung, die Stutzenlasten über Druckdosen (D1 bis D4, vgl. Bild 3) aufgebracht. Der Versuchsaufbau bildete während der gesamten Versuchsdauer ein geschlossenes Kräftesystem und konnte deshalb nahezu zwä;ngungsfrei gelagert werden.
Die Stutzen wurden so gewählt, daß sie ein möglichst breites Spektrum der Parameterstudie abdecken. An den Versuchskörpern wurden Zugversuche zur Ermittlung des Steifemoduls durchgeführt. Die Form und die Wanddicken der Versuchskörper wurde vermessen. Dabei wurde festgestellt, daß insbesondere die Wanddicken in der Krempe der Behälterböden sehr stark veränderlich sind. Die vergleichende Berechnung der Versuche erfolgte mit der gemittelten – rotationssymmetrischen – Form der Behälterböden mit konstanter Wanddicke. Die Randbedingungen der FE-Berechnung wurden dabei soweit als möglich und sinnvoll gleich zu denen der elastischen Parameterstudie abgebildet. Die Abbildung der Stutzen in der FE-Berechnung erfolgte entsprechend der nachvermessenen Lage der Stutzen.
Die Auswertung der Dehnungs- und Verschiebungsmessungen bestätigte - im Rahmen der möglichen Fehlerquellen bei der Versuchsdurchführung - die vergleichende FE-Berechnung und damit auch die Annahmen und die Idealisierung der elastischen Parameterstudie.
4. Statischer Festigkeitsnachweis
Die Beanspruchungen an den maßgebenden Schnitten werden entsprechend [3] als lokale Membran- (Pl) und sekundäre Biegespannung (Q) eingeordnet. Die Definition der bewerteten Vergleichspannung bei der Auswertung der elastischen Parameterstudie
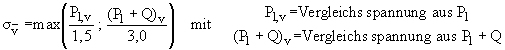 (1)
(1)
führt mit den Beanspruchungsgrenzen nach [3]
Pl £ 1,5×f und Pl+Q £ 3×f (f = K/S: zulässige Berechnungsspannung nach [5]) (2)
zu der einfachen Nachweisform
Bei vorgegebener Geometrie und Belastung kann die bewertete Vergleichsspannung und die Steifigkeit und Modellabbildung des Stutzenanschlusses (vgl. Bild 1) direkt dem Interpolationsprogramm entnommen oder indirekt aus Diagrammen bestimmt werden. Der Vergleichsspannung liegt dabei die Gestaltänderungs-Energiehypothese zugrunde. Bei der Beschreibung der Geometrie des Stutzenanschlusses müssen dabei eventuelle Wanddickenminderungen nach [6] (Wanddickenunterschreitung und Abnutzung) berücksichtigt werden. Zur Bestimmung von Zwängungskräften aus den an den Stutzen anschließenden Rohrleitungen werden die Anschlußsteifigkeiten des Stutzens und dessen Modellabbildung benötigt (vgl. Bild 1).
5. Ermüdungsversuche
Die Versuchskörper wurden voneinander getrennt und bei vertikaler Stutzenachse am Flansch gehalten. Die Belastung der Stutzen erfolgte mit einer wechselnden vertikalen Last, die im Abstand von 1,505m (VK1, Stutzen "S3") und 1,50m (VK2, Stutzen "S1") von der Stutzenachse auf die Lasttraverse wirkte. Die Versuche wurden im Low-Cycle-Fatigue Bereich durchgeführt. Der Anriß bei den Schweißnähten der Stutzenanschlußstellen wurde bei 500 bzw. 21600 Lastspielen unter Verwendung des Magnetpulververfahrens festgestellt. Der erste Anriß wurde bei beiden Stutzenanschlüssen an der Nahtübergangskerbe an der Außenseite der Behälterböden auf der Kalottenseite der Verschneidungslinie festgestellt. Die Anzahl der Lastspiele bis zum ersten Anriß entsprachen bei beiden Stutzenanschlußstellen im Rahmen der üblichen Streuung dem Ergebnis des nachfolgend vorgestellten Konzepts der Ermüdungsfestigkeit und bestätigten dieses.
6. Nachweis der Ermüdungsfestigkeit
Aus der elastischen Parameterstudie ergeben sich die Strukturspannungen an den maßgebenden Schnitten. Aus diesen Strukturspannungen (s^, s|| und t) lassen sich mit der Kerbformzahl rechtwinklig zur Schweißnaht der Verschneidung a^ von Stutzen und Behälterboden die Kerbspannungen (s^,K, s||,K und tK) und daraus die Kerbvergleichsspannung (sv,K) ermitteln:
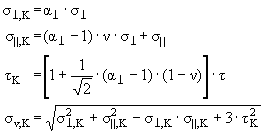 (4)
(4)
Die Kerbformzahl ist für jeden Einzelfall vom Anwender zu ermitteln. Für Kerbformzahlen a^ =2, 3, 4, 5, 7 oder 10 kann bei gegebener Geometrie und Belastung die Kerbvergleichsspannung direkt dem Interpolationsprogramm entnommen oder indirekt aus Diagrammen bestimmt werden. Mit der Kerbvergleichsspannung kann anschließend ein Ermüdungsnachweis mit dem Kerbgrundkonzept geführt werden.
7. Beispiel
Die Geometrieparameter des Stutzens "S1" sind Da=80cm, ca/Da=0.4894, di/Da=0.11, se/Da=0.0125 und ss/se=1.0. Die Belastung des Stutzens S2 bei den Ermüdungsversuchen betrug Fz=± 2kN und My=± 300kNcm. Die für den statischen Nachweis benötigte bewertete Vergleichsspannung bei der Lastschwingbreite D Fz=4kN und D My=600kNcm [4, Abschnitt 6.3] ergibt sich aus der auf der sicheren Seite liegenden Überlagerung beider Einzellastfälle (Tab. 2).

Die Versuchsbelastung entspricht in etwa der zulässigen Belastung (16,1» f=24kN/cm2/1,5 mit K=24kN/cm2 und S=1,5). Zur Abschätzung der Ermüdungsneigung muß zuerst die Kerbformzahl für jeden Einzelfall ermittelt werden. Dazu wird eine Finite-Elementberechnung mit dem Programm ANSYS, Version 5.3 unter Verwendung des 8-knotigen Scheibenelementes Plane82 und der Option für den ebenen Dehnungszustand durchgeführt. Die Ausrundung der Kerben zur Berücksichtigung der Mikrostützwirkung des Materials wird mit 1mm [7] angesetzt. Die Belastung erfolgt über ein Moment an dem oberen, freien Rand des FE-Modells. Der Kerbfaktor ergibt sich aus dem Verhältnis der Maximalspannung in der Kerbe zu der Biegerandspannung der verbundenen Bauteile. Bei der Berechnung konnte festgestellt werden, daß bei den Abmessungsverhältnissen der Versuchskörper die Kerbfaktoren an den Orten 1, 2 und 3 nur unwesentlich von dem Verbindungswinkel der Bauteile und den Schweißnahtdicken abhängen (vgl. Bild 4). Der Kerbfaktor ergibt sich für die Orte 1 und 2 näherungsweise zu a^,1,2=2.0 und am Ort 3 zu a^,3=1.8.
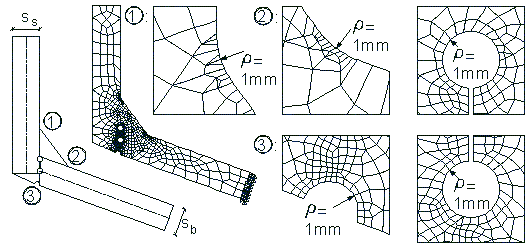
Im folgenden wird die Untersuchung auf den Ort beschränkt, bei dem in den Versuchen der erste Anriß auftrat. Mit dem Interpolationsprogramm werden die zu der Lastamplitude gehörigen Kerbvergleichsspannungen an der Behälterschale außen ermittelt (Tab. 3).

Der Zusammenhang zwischen den Dehnungen und der elastizitätstheoretischen Kerbvergleichsspannung läßt sich mit der Neuberschen Makrostützwirkung abschätzen. Die zugrundeliegende zyklische Werkstoffkennlinie wurde entsprechend Ramberg-Osgood für unlegierte und niedriglegierte Stähle angenommen [8]. Daraus ergibt sich die am Ort des Versagen zu erwartende Dehnungsamplitude zu 0,376 Prozent (vgl. Bild 5).

Für den Werkstoff der Behälterböden (Kesselblech H II) werden die elastisch-plastischen Dehnungswöhlerlinien ermittelt [9]:
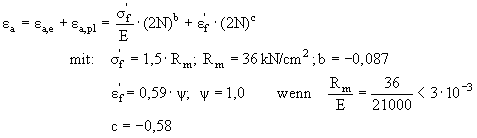 (5)
(5)
Die bei 21600 Lastspielen zum Anriß führende Kerbdehnung von 0,376 Prozent wird mit den elastisch-plastischen Dehnungswöhlerlinien [9] und der für den Kerbspannungsnachweis nach [10] anzuwendenden Wöhlerlinie FAT 225 verglichen (vgl. Bild 6). Dieser Vergleich zeigt, daß bei den Annahmen zum Nachweis der Ermüdungsfestigkeit der erste Anriß . bereits früher, bei etwa 6000 Lastspielen, zu erwarten gewesen wäre. Dieser Effekt läßt sich auf die Annahmen der elastischen Parameterstudie und auf die Vorgehensweise bei der Nachweisführung zurückführen:
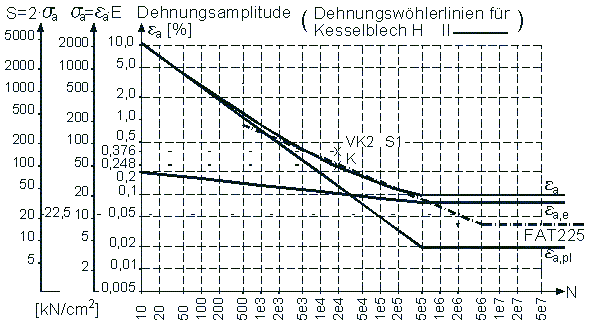
Der Einfluß der auf der sicheren Seite liegenden Annahme der elastischen Parameterstudie, bei der die Beanspruchungen an den maßgebenden Schnitten und nicht am Ort der Nahtübergangskerbe ausgewertet werden, wird abgeschätzt, indem der Durchmesser des Stutzens um den doppelten Wert der Schweißnahtbreite – etwa 20mm – vergrößert wird. Die Geometrieparameter des derart aufgeweiteten Stutzens ergeben sich zu Da=80cm, ca/Da=0.4894, di/Da=0.135, se/Da=0.0125 und ss/se=1.0. Die Kerbvergleichsspannung aus dem Interpolationsprogramm ergibt sich dann bei a^ =2.0 zu 32.3+1.0=33.3kN/cm2. Aus der Neuberschen Makrostützwirkung und der zyklischen Werkstofflinie nach Ramberg-Osgood ergibt sich die Dehnungsamplitude zu 0.248 Prozent. Im Bild 6 ergibt sich dann die Korrektur zum Punkt K, der im Rahmen der Meßgenauigkeit gleichzeitig auf der Dehnungswöhlerlinie nach [9] und auf der Wöhlerlinie FAT225 nach [10] liegt.
Der Einfluß der auf der sicheren Seite liegenden Überlagerung in der Nachweisführung ist in diesem Beispiel nur untergeordnet, weil die Maximalwerte der Beanspruchungen der Einzellastfälle Fz und My an der selben Stelle der Verschneidunglinie wirken und weil die dort wirkenden Spannungskomponenten der Einzellastfälle in etwa im gleichen Verhältnis zueinander stehen. Bei anderen Lastfallkombinationen kann dieser Einfluß größer sein.
8. Zusammenfassung
Mit den Ergebnissen der beiden hier vorgestellten Forschungsvorhaben und dem dabei entwickelten, frei verfügbaren Interpolationsprogramm vereinfacht sich sowohl der statische Nachweis als auch die Absicherung gegen Ermüdungsbrüche von Stutzenanschlußstellen auf eine einfache Handrechnung. Die Ergebnisse dieser Forschungsvorhaben beseitigen den bislang bestehenden Wettbewerbsnachteil kleinerer und mittelständischer Unternehmen und sichern eine Weiterführung der bisher in Deutschland üblichen Praxis von Stutzen im Krempenbereich gewölbter Böden im europäischen Umfeld.
Schrifttum:
[1] H. Saal und H. Bauer (08/1995), "Schlußbericht zum Forschungsvorhaben AiF-8577: Festigkeitsnachweise von Stutzenanschlußstellen im Krempenbereich gewölbter Böden unter Berücksichtigung der Einwirkung von Stutzenlasten", Fraunhofer IRB-Verlag
[2] H. Saal und H. Bauer (02/1997), "Schlußbericht zum Forschungsvorhaben AiF 10766 N/1: Festigkeitsnachweise von Stutzenanschlußstellen im Krempenbereich gewölbter Böden unter Berücksichtigung der Einwirkung von Stutzenlasten mit Erweiterung auf Ermüdungsfestigkeit", Lehrstuhl für Stahl- und Leichtmetallbau, Universität Karlsruhe, 76128 Karlsruhe
[3] AD-Merkblatt B9 (07/1995), "Ausschnitte in Zylindern, Kegeln und Kugeln unter innerem Überdruck", VdTÜV Essen
[4] AD-Merkblatt S4 (02/1998), "Bewertung von Spannungen bei rechnerischen und experimentellen Spannungsanalysen", VdTÜV Essen
[5] AD-Merkblatt S3/0 (01/1995), "Allgemeiner Standsicherheitsnachweis für Druckbehälter: Grundzüge", VdTÜV Essen
[6] AD-Merkblatt B0 (01/1995), "Berechnung von Druckbehältern", VdTÜV Essen
[7] D. Radaj (1995), "Ermüdungsfestigkeit", Springer Verlag
[8] T. Seeger, P. Zacher (1994), "Lebensdauervorhersage zwischen Traglast und Dauerfestigkeit am Beispiel ausgeklinkter Träger", Bauingenieur 69, S. 13-23, Springer Verlag
[9] Chr. Boller & Z. Seeger (1987), "Materials Data for Cyclic Loading (Part A)", Elsevier Verlag
[10] Hobbacher (1997), "Empfehlungen zu Schwingfestigkeit geschweißter Verbindungen und Bauteile, IIW-Document XIII-1539-96 / XV-845-96", DVS-Verlag